特征值分解（Eigenvalue Decomposition）和奇异值分解（Singular Value Decomposition, SVD）是线性代数中两个核心的矩阵分解方法，它们的区别可以从通俗角度理解为以下几个方面：

1.适用对象不同

特征值分解：  

  只适用于方阵（行数=列数），且矩阵必须是对角化的（比如对称矩阵）。  

  通俗比喻：像一把钥匙只能开特定的锁，必须是“正方形”且满足条件才能分解。

奇异值分解：  

  适用于任意形状的矩阵（长方形、正方形均可），无论矩阵是否可对角化。  

  通俗比喻：像一把万能钥匙，能处理所有形状的矩阵，甚至是“残缺不全”的数据。

2. 物理意义不同

特征值分解：  

  描述矩阵对**向量方向的缩放作用。  

  例子：如果矩阵代表一个物理变换（如旋转或缩放），特征值表示缩放倍数，特征向量表示变换后方向不变的方向。

奇异值分解：  

  描述矩阵对**空间的双向作用**（行空间和列空间）。  

例子：如果矩阵是一张图片（像素矩阵），SVD可以将图片分解为“主要特征”（奇异值大的部分）和“细节”（奇异值小的部分），用于压缩或去噪。

3. 分解结果的组成不同

特征值分解：  

  将方阵分解为：  

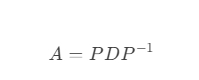
  其中，P是特征向量组成的矩阵，D是对角矩阵（对角线为特征值）。

奇异值分解：  

  将任意矩阵分解为：  

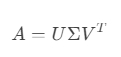
  其中，U和 V是正交矩阵（列向量是正交单位向量），\(\Sigma\) 是包含奇异值的对角矩阵。

4. 应用场景不同

特征值分解：  

分析物理系统的稳定性（如特征值实部是否小于零）。  

主成分分析（PCA）的原始实现（但实际常用SVD）。  

 振动分析（如机械结构的固有频率）。

奇异值分解：  

数据降维（如PCA底层依赖SVD）。  

图像压缩（保留前几个大奇异值即可重构主要信息）。  

推荐系统（用户-物品评分矩阵分解）。  

自然语言处理（潜在语义分析LSA）。

5. 数值稳定性不同

特征值分解：  

  对非对称矩阵或病态矩阵（如接近不可逆的矩阵）敏感，计算可能不稳定。

奇异值分解：  

  数值稳定性更高，即使矩阵存在噪声或接近奇异，SVD仍能提供可靠结果。

通俗总结

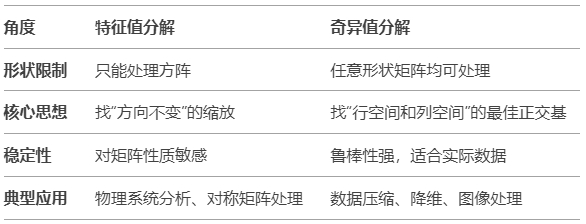
举个栗子 

假设你有一组数据点分布在平面上：

特征值分解：告诉你沿着哪些方向拉伸或压缩数据（如椭圆的长轴和短轴方向）。  

奇异值分解：不仅告诉你拉伸方向，还能处理数据分布倾斜的情况（比如把倾斜的椭圆“摆正”）。

一句话记忆

特征值分解是“方阵的专属工具”，研究方向不变的缩放。  

奇异值分解是“万能瑞士军刀”，通过**双向正交基拆解任意矩阵。