在图像处理领域，QR分解与LU分解凭借其独特的数学特性，分别适用于不同的应用场景。以下是对这两种分解方法的比较及其典型应用的分析：

QR分解

特点：

正交性：QR分解将矩阵分解为正交矩阵Q和上三角矩阵R，有利于保持向量间的正交关系。

数值稳定性：对于病态矩阵，QR分解具有更强的鲁棒性，适用于高精度计算。

最小二乘解：QR分解能够有效处理超定方程组，如拟合问题。

应用场景：

1. 图像配准与几何校正：通过求解超定方程组来估计变换参数（例如仿射变换）。

2. 特征提取与PCA：通过正交化过程提取主成分，用于降维或识别。

3. 结构分析：利用QR算法计算矩阵特征值，用于纹理或边缘方向分析。

4. 自适应压缩：通过构造正交基实现能量集中，提高压缩效率（如在特定矩阵分解步骤中）。

LU分解

特点：

高效解方程：LU分解将矩阵分解为下三角矩阵L和上三角矩阵U，便于快速求解线性系统。

适用于方阵：主要处理方阵问题，计算速度较快。

内存优化：特别适合稀疏矩阵，能够减少存储需求。

应用场景：

1. 图像去模糊与复原：通过求解大型线性系统（如泊松方程）实现去卷积。

2. 实时滤镜处理：快速解局部线性方程组（如颜色调整、噪声消除）。

3. 图像混合与编辑：高效计算像素级操作中的逆变换或调整。

4. 矩阵求逆加速：在需要频繁求逆的算法中（如某些滤波算法）提高效率。

对比总结

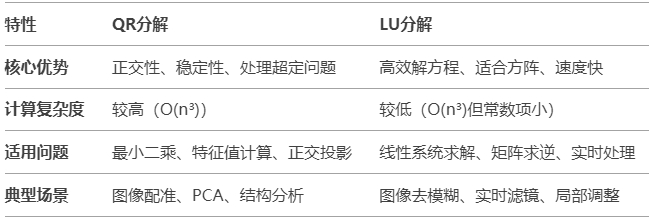
通过上述对比，我们可以看到QR分解和LU分解在图像处理中的应用各有侧重，根据具体问题选择合适的分解方法对于优化算法性能至关重要。

分析：文章对比了QR分解和LU分解在特定应用场景下的表现。QR分解在需要稳定性和正交性的任务中效果显著，例如参数估计和降维。相对而言，LU分解在追求计算效率和方阵求解方面表现更佳，适用于实时处理和图像复原等场合。在实际应用中，应根据问题的性质、矩阵的特性以及计算资源等因素来决定使用哪种分解方法。

改写：在追求稳定性和正交性的任务中，如参数估计和降维，QR分解显示出其卓越的性能。而LU分解在追求计算效率和解决方阵问题时更胜一筹，特别适用于实时处理和图像复原等领域。在实际应用中，应根据问题的具体要求、矩阵的特性以及可用的计算资源，合理选择使用QR分解或LU分解。